超高速 In-Place Merge Sort （クイックソートに匹敵する速度のインプレースマージソート）

クイックソートに匹敵する速度へ (クイックソートが最速という常識への挑戦)

一般のマージソートでは，データの記憶領域と同じ程度の追加の記憶領域が必要です。in-place merge sort（インプレースマージソート）とは，追加の記憶領域をほとんど使わずに行うマージソートです。
また，一般のマージソートでは，キーの値が同じ要素のソー ト前の順序が，ソート後も変わらずに維持されます。このようなソートを安定ソートと言います。
一般のマージソートは，最速と言われているクイックソートよりも遅いようです。ただし，クイックソートは，安定ソートではありません。（私が作ったマージソートはクイッ クソートよりも速いです。）
これまでのインプレースマージソートの研究目標の多くは，安定ソートでありながら平均計算時間と最悪計算時間が共にO(n (log n)で一般のマージソート並みの速さのものを作ることだったようです。

In-Place Sorting With Merge Sort に，平均計算時間と最悪計算時間が共に O(n log n)で，安定ソートではないインプレースマージソートがありますが，それは一般のマージソートより遅いものです。
私も，平均計算時間と最悪計算時間が共に O(n log n)で，安定ソートではないインプレースマージソートを作りました。再帰呼 び出しを用いていて，追加の記憶領域は O(log n) です。（2025年１月）
その後，改良を重ねたところ，大量のランダムなデータに対する平均計算時間はクイックソートに匹敵するまでになりました。
そのソートは，In-Place Sorting With Merge Sort にあるインプレースマージソートを基本として，それに幾つかの速度を上げる改良を施した形になっています。
In-Place Sorting With Merge Sort での計算時間O(n log n)のインプレースマージソートの実現方法と，このインプレースマージソートを比較しながら，以下を読んで頂ければ幸いです。

ここで示すインプレースマージソートは，In-Place Sorting With Merge Sort にあるインプレースマージソートよりも高速ですが，それは，部分列のソート法を次のように変えたからです。
    データ列のある部分をソートする　→　データ列のある部分をソートされたデータ列にする
ここでは，データ列のある部分について，そこに存在するデータをソートするのではなく，その部分を，他の部分にあるデータも用いてソートされたデータ列に したのです。

In-Place Sorting With Merge Sort では，整列されたm個のデータと整列されたk個のデータを，整列されていないk個のデータを上手く用いて，整列されたm+k個のデータにしていました。
    (整列されたm個，整列されていないk 個，整列されたk個)　→　(整列されたm+k個，整列されていないk個)
ここでのインプレースマージソートは，上記の操作を再帰的に繰り返しました。このことが，In-Place Sorting With Merge Sort のソート法より高速になった最大の理由と思われます。

さらに，ソートされていないデータ が少なくになったとき，ソートされていないデータをソートされたデータ列にマージするのに新たな手法を用いました。
これにより，クイックソートやイントロソートに匹敵する速度までになりました。
また，小さなデータブロックに対するソートに挿入ソートを用いることにより高速化しましたが，クイックソートもこの方法で同様に高速化されます。
このソートは，最悪計算時間において，クイックソートやイントロソートよりも優れていて，私の知る限りインプレースなソートの内では最悪計算時間において 最も優れています。

インプレースマージソートを少しでも高速化しようと工夫していましたが，ほんの少し高速化するとコードが長く 複雑になることに気が付きました。
そこで，コードの複雑さを極力抑えて，短いコードで世界最速を目指しました。そのコードを示しま す。


世界最速のソートアルゴリズムを目指したインプレースマージソートのコード
ランダムなデータに対してクイックソートとほぼ同じ速度を実現したコードです。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int d_type;// ソートするキーの型

//挿入ソート
#define INSERTION_SORT\
    for (;i<n;i++){\
        d_type tmp=array[i];\
        int j=i-1;\
        for (;j>=0 && array[j]>tmp;j--) array[j+1]=array[j];\
        array[j+1]=tmp;\
    }

//値を交換する関数
void swap(d_type *x,d_type *y){
    d_type tmp=*x;
    *x=*y;
    *y=tmp;
}

// マージ (整列されたm個，整列されていないk 個，整列されたk個)
//　→　(整列されたm+k個，整列されていないk個) を行う関数
void mergeD(d_type a[], int m, int k){
    d_type *b=a+(m-1),*c=a+(m-1)+k,*d=a+(m-1)+2*k;
    while (1) {
        if (*b>*d) {
            swap(b,c);
            b--;c--;
            if (b<a) {
                while(c>=a){
                    swap(c,d);
                    c--;d--;
                }
                break;
            }
        } else {
            swap(c,d);
            c--;d--;
            if (c<=b) break;
        }
    }
}

#define RATIO 0.2 //RATIO<=0.5
//整列されたn個の要素の配列を作る関数
void merge_sortD(d_type array[], int n){
    if (n<50) {
        int i=1;
        INSERTION_SORT
        return;
    }
    int k=n*RATIO,m=n-k;//k=n/2をk=n*0.2に変えたら，なぜか高速化
    merge_sortD(array,m);
    merge_sortD(array+n,k);
    mergeD(array,m,k);
}

#define SWAP(x,y) if (array[x]<array[y]) swap(array+x,array+y);

void merge_sort(d_type array[], int n){
    int m=n*(1.0-RATIO);//mをできるだけ大きくした
    merge_sortD(array,m);//整列されたm個の要素の配列を作る
    int k=(n-m)/2,i=m;
    while (k>=3){//m個の要素の配列にk個の要素をマージすることを繰り返す
        int end=m+k-3;
        for (;i<=end;i++) {int j=i+2;SWAP(i,j);SWAP(i+1,j);SWAP(j,i+k)}
        merge_sort(array+m+k,n-m-k);
        mergeD(array,m,k);
        m=m+k;
        k=(n-m)/2;
        i=m;
    }
    INSERTION_SORT //残った要素を挿入ソートする
}
#undef SWAP
#undef RATIO
#undef INSERTION_SORT

int main(){
    int n=100000000;
    int i;
    clock_t start,end;
    d_type *array=malloc(n*sizeof(d_type));
    srand((unsigned) time(NULL));
    for (i=0;i<n;i++) array[i]=rand()*(RAND_MAX+1)+rand();
    start=clock();
    merge_sort(array,n);
    end=clock();
    printf("%f秒  \n",(double)(end-start)/CLOCKS_PER_SEC);
    for (i=1;i<n;i++) if(array[i-1]>array[i]) printf("%d %d\n",i,array[i]);
    free(array);
    return 0;
}

上記の merge_sort() は，基本的なコードに次のコードを付加することにより，大きく高速化されています。
高速化のために付加した次のコードは，ソートされていない残ったデータのうちで，小さい値のデー タをなるべく早くマージするためのものです。無くても動作しますので，速度を比較してみてください。

        int end=m+k-3;
        for (;i<=end;i++) {SWAP(i,i+2);SWAP(i+1,i+2);SWAP(i+2,i+k)}

上記のプログラムがやっていることの概略は，次の様です。

1　全データの80％分のソートされた配列を作る。(この作業は，関数 merge_sortD() により高速に行われる)
2　残りの20％のうちの半分の10％をソートされた配列にし，それをソートされた80％の配列にマージして，ソートされた90％分の配列を作る。
3　残りの10％のうちの半分の5％をソートされた配列にし，それをソートされた90％の配列にマージして，ソートされた95％分の配列を作る。
4　残りの5％のうちの半分の2.5％をソートされた配列にし，それをソートされた95％の配列にマージして，ソートされた97.5％分の配列を作る。
          …………

最初のコードでは，できるだけデータ数がほぼ等しいデータ群をマージしようとしていました。すなわち，m≒k となる割合を多くすれば高速になると思い込んでいました。
ところが，コードの一部の「k=n/2」を「k=n*0.2」に変えたところ，不思議にも大きく速くなりました。
データ数比 1：1でマージしていたのを，4:：1でマージするように変えると遅くなると思っていたのに，速くなるなんてびっくり。
私には理由は分かりませんが，「クイックソートのピボットは中央値でなく四分位数を選択したほうが高速」というブログを見て，もしかしたら分岐予測ミス確 率の関係かなと思っています。

注　RATIO の値は0.2としていますが，もっと細かく，0.19や0.18とすると，実行するコンピュータによっては少しだけ高速になるかもしれません。

最悪計算時間がO(n log n) となることは，次の様に分かります。
　①　ほぼ同じ大きさのデータをマージする操作の計算時間の合計はO(n log n) で抑えられる。
　②　大きさが大きく異なるデータをマージする回数はO(log n)で抑えられるから，それらの計算時間の和はO(n log n) で抑えられる。
　③　高速化のテクニックは計算時間を減少させるだけである。

注　関数 merge_sort() にある「m=n*(1.0-RATIO);//mをできるだけ大きくした」は，関数 merge_sortD()を用いるに当たり，次の条件が満たされれば良いと考えたからです。
    m+m×RATIO+m×(RATIO)2+m×(RATIO)3+m×(RATIO)4+……≦n
ここで，無限等比級数の和の公式により
    左辺=m/(1-RATIO)
よって
    m/(1-RATIO)≦n
となるから
    m≦n×(1-RATIO)


1つ前の方法のコード
次のコードは，上記のコードの関数 merge_sort() の高速化法の1つ前の方法で書いたもので，上記のコードより僅かに遅いです。

void merge_sort(d_type array[], int n){
    int m=n*(1.0-RATIO);//mをできるだけ大きくした
    merge_sortD(array,m);
    int k=(n-m)/2,border=n/60,i=m;
    while (k>=2){
        if (k>=border)
            merge_sortD(array+m,k);
        else
            merge_sort(array+m,n-m);
        int end=m+k;
        for (;i<end;i++) swap(array+i,array+i+k);
        mergeD(array,m,k);
        m=end;
        k=(n-m)/2;
    }
    INSERTION_SORT
}

このコードでは， k<border のときに小さい要素だけがマージされます。その基本的なアイデアは次の様です。

    (整列されたm個，整列されていない2k 個) → (整列されたm個，整列されていないk個，整列されたk個) → (整列されたm+k個，整列されていないk個)
と変形するときに，整列されたk個の要素の全てが，整列されていないk個のどの要素よりも大きく無いようにしたい。
そうすれば，整列されたm+k個の要素の半数位は，整列されていないk個のどの要素よりも大きく無くなるから，次に整列されていないk個を処理するときに 高速化される。
そのためには，整列されていない2k個の要素を整列されていないk個と整列されたk個の要素に分けるときに，このインプレースマージソート自身を用いれば よい。


クイックソートとの比較
「クイックソートは世界最速のソートアルゴリズム」と言われることがありますが，素朴なままのクイックソートのコードでは上記のインプレースマージソートより遅いです。
そこで，私ができるだけの高速化をしたクイックソートのコードを作り，世界最速のソートアルゴリズムを目指したインプレースマージソートのコードと計算時間の比較をすることにしました。
私のパソコンで計測したところでは，このインプレースマージソートの１億個のランダムなデータに対する平均計算時間は，クイッ クソートと同じくらいです。
実際にコンパイルして実行してみて下さい。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int d_type;// ソートするキーの型

#define INSERTION_SORT\
    for (;i<n;i++){\
        d_type tmp=array[i];\
        int j=i-1;\
        for (;j>=0 && array[j]>tmp;j--) array[j+1]=array[j];\
        array[j+1]=tmp;\
    }

void swap(d_type *x,d_type *y){
    d_type tmp=*x;
    *x=*y;
    *y=tmp;
}

void mergeD(d_type a[], int m, int k){
    d_type *b=a+(m-1),*c=a+(m-1)+k,*d=a+(m-1)+2*k;
    while (1) {
        if (*b>*d) {
            swap(b,c);
            b--;c--;
            if (b<a) {
                while(c>=a){
                    swap(c,d);
                    c--;d--;
                }
                break;
            }
        } else {
            swap(c,d);
            c--;d--;
            if (c<=b) break;
        }
    }
}

#define RATIO 0.2 //RATIO<=0.5
void merge_sortD(d_type array[], int n){
    if (n<50) {
        int i=1;
        INSERTION_SORT
        return;
    }
    int k=n*RATIO,m=n-k;//k=n/2をk=n*0.2に変えたら，なぜか高速化
    merge_sortD(array,m);
    merge_sortD(array+n,k);
    mergeD(array,m,k);
}

#define SWAP(x,y) if (array[x]<array[y]) swap(array+x,array+y);

void merge_sort(d_type array[], int n){
    int m=n*(1.0-RATIO);//mをできるだけ大きくした
    merge_sortD(array,m);//整列されたm個の要素の配列を作る
    int k=(n-m)/2,i=m;
    while (k>=3){//m個の要素の配列にk個の要素をマージすることを繰り返す
        int end=m+k-3;
        for (;i<=end;i++) {int j=i+2;SWAP(i,j);SWAP(i+1,j);SWAP(j,i+k)}
        merge_sort(array+m+k,n-m-k);
        mergeD(array,m,k);
        m=m+k;
        k=(n-m)/2;
        i=m;
    }
    INSERTION_SORT //残った要素を挿入ソートする
}
#undef SWAP
#undef RATIO

void insertion_sort(d_type array[],int n){
    int i=1;
    INSERTION_SORT
}
#undef INSERTION_SORT

d_type med3(d_type x,d_type y,d_type z){
    if (x<y){
        if (y<z)      return y;
        else if (z<x) return x;
    }else{
        if (z<y)      return y;
        else if (x<z) return x;
    }
    return z;
}

void quick_sort(d_type array[], int begin, int end){
    int n=end-begin;
    if (n<50){
        insertion_sort(array+begin,n+1);
        return;
    }
    d_type pivot=med3(array[begin],array[begin+n/2],array[end]);
    int l=begin,r=end;
    while(1){
        while(array[l]<pivot) l++;
        while(array[r]>pivot) r--;
        if(l>=r) break;
        swap(array+l,array+r);
        l++;r--;
    }
    quick_sort(array,begin,r);//l=r+1
    quick_sort(array,r+1,end);
}

int main(){
    int n=100000000;
    int i;
    clock_t start,end,end2;
    d_type *array=malloc(n*sizeof(d_type));
    d_type *array2=malloc(n*sizeof(d_type));
    srand((unsigned) time(NULL));
    for (i=0;i<n;i++){
        array[i]=rand()*(RAND_MAX+1)+rand();
        array2[i]=array[i];
    }
    start=clock();
    merge_sort(array,n);
    end=clock();
    quick_sort(array2,0,n-1);
    end2=clock();
    printf("merge_sort %f秒  \n",(double)(end-start)/CLOCKS_PER_SEC);
    printf("quick_sort %f秒  \n",(double)(end2-end)/CLOCKS_PER_SEC);
    for (i=0;i<n;i++) if(array[i]!=array2[i]) printf("%d %d\n",array[i],array2[i]);
    free(array);
    free(array2);
    return 0;
}

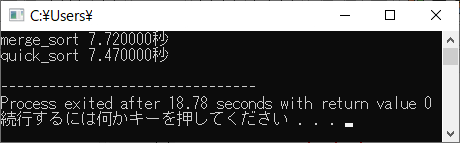
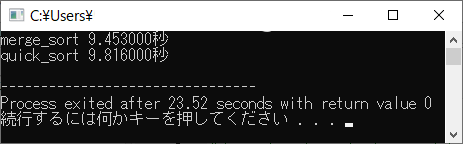
実行例
2台のパソコンで実行してみました。

       実行例           実行例2


イントロソートとの比較
イントロソートは，このインプレースマージソートと同じく，平均計算時間と最悪計算時間が共に O(n log n)の非安定なインプレースソートです。
したがって，このソートの比較対象は，クイックソートよりもイントロソートの方が適切ではないかと考えます。
イントロソートは，クイックソートよりもコードが長く複雑で，平均計算時間はクイックソートよりも少しだけ長くなります。
このインプレースマージソートは，コードの長さはイントロソートよりやや短いくらいで，平均計算時間はクイックソートと同じくらいです。
したがって，このインプレースマージソートはイントロソートに対して，コードがやや短く，ランダムのデータに対する平均計算時間はやや短いです。

最悪計算時間は，クイックソートはO(n2)で，イントロソートとヒープソートはO(n log n)です。
イントロソートは，最悪の場合に途中からヒープソートに切り替えるため，最悪計算時間はヒープソートの最悪計算時間より長くなります。
ヒープソートは，平均計算時間がO(n log n)のソートの内で比較的遅いソートです。
したがって，このインプレースマージソートは，データ数が多いときの最悪計算時間が最短だと考えられます。

以上のことから，このインプレースマージソートは，最悪計算時間がO(n log n)であるインプレースソートのうちで最速だと結論します。
以下に，イントロソートのコードを示しますので，実際に実行して，このインプレースマージソートと比較してみてください。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

typedef int d_type;// ソートするキーの型

void swap(d_type *x,d_type *y){
    d_type tmp=*x;
    *x=*y;
    *y=tmp;
}

void insertion_sort(d_type array[],int n) {
    int i=1;
    for (;i<n;i++){
        d_type tmp=array[i];
        int j=i-1;
        for (;j>=0 && array[j]>tmp;j--) array[j+1]=array[j];
        array[j+1]=tmp;
    }
}

void downheap(d_type *array,d_type work,int parent,int child,int last) {
    while (1) {
        if (child<last) {
            if (array[child+1]>array[child]) child++;
        } else if (child>last) {
            break;
        }
        if (work>=array[child]) break;
        array[parent]=array[child];
        parent=child;
        child=2*parent+1;
    }
    array[parent]=work;
}

void heap_sort(d_type *array, int last) {
    int i;
    for (i=(last-1)/2;i>=0;i--) {
        downheap(array,array[i],i,2*i+1,last);
    }
    for (i=last;i>0;) {
        d_type work=array[i];
        array[i]=array[0];
        downheap(array,work,0,1,--i);
    }
}

d_type med3(d_type x,d_type y,d_type z){
    if (x<y){
        if (y<z)      return y;
        else if (z<x) return x;
    }else{
        if (z<y)      return y;
        else if (x<z) return x;
    }
    return z;
}

void safe_quick_sort(d_type *array,int begin,int end,int maxDepth) {
    int range=end-begin;
    if (range<50){
        insertion_sort(array+begin,range+1);
        return;
    }
    if (maxDepth<=0){
        heap_sort(array+begin,range);
        return;
    }
    d_type pivot=med3(array[begin],array[begin+range/2],array[end]);
    int l=begin,r=end;
    while(1){
        while(array[l]<pivot) l++;
        while(array[r]>pivot) r--;
        if(l>=r) break;
        swap(&array[l],&array[r]);
        l++;r--;
    }
    maxDepth--;
    safe_quick_sort(array,begin,r,maxDepth);//l=r+1
    safe_quick_sort(array,r+1,end,maxDepth);
}

void intro_sort(d_type *array,int n) {
    int M=1,maxDepth=0;
    while (M<n) {
        M=M*2;
        maxDepth=maxDepth+2;
    }
    safe_quick_sort(array,0,n-1,maxDepth);
}

int main(){
    int n=100000000;
    int i;
    clock_t start,end;
    d_type *array=malloc(n*sizeof(d_type));
    srand((unsigned) time(NULL));
    for (i=0;i<n;i++){
        array[i]=rand()*(RAND_MAX+1)+rand();
    }
    start=clock();
    intro_sort(array,n);
    end=clock();
    printf("%f秒  \n",(double)(end-start)/CLOCKS_PER_SEC);
    for (i=1;i<n;i++) if(array[i-1]>array[i]) printf("%d %d\n",i,array[i]);
    free(array);
    return 0;
}


理由が大して分からずマジックのように速くなったソートなので，冗談でマジックソートとでも名前をつけたくなります。マージソートの考案者のフォン・ノイ マンもマジマジと見ているかもしれません。

最初のページ に戻る