問題と大学による解説は,次のリンクにあります。 理科問題(物理)〔3〕Aの解説
問1についての疑問
音叉を囲む円周上にある4つの点A~Dでの空気の疎密に関する問題ですが,以下の論拠により,該当する選 択肢がないように思えます。
音波は伝わっていくときに,空気が密な位置は,その両側から空気分子が寄ってくる位置で,空気が疎な位置は,その両側へ空気分子が離れて行く位置です。音 波が伝わる方向を正の方向とするとします。正弦波では,空気が密になるのは,空気の変位が正から負に変わる位置となり,空気が疎になるのは,空気の変位が 負から正に変わる位置となります。正確には,変位を表すグラフの接線の傾きが負である位置は密になり,接線の傾きが正である位置は疎になります。
したがって,下にある空気の密度を表すグラフは,空気の変位を表すグラフを微分して-1倍したものです。
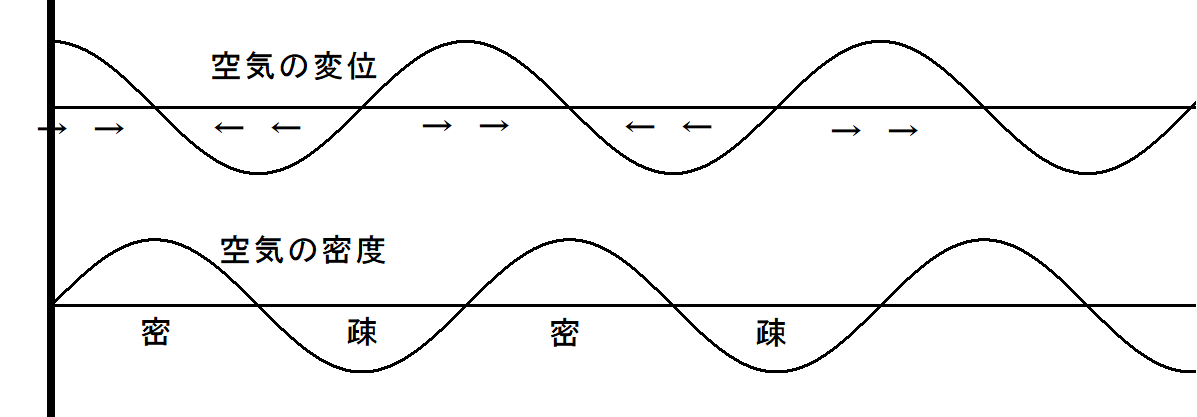
さて,音叉の腕が運動し,開ききったとき,音叉の付近の空気分子の変位は,正の向きに最大になります。問題図の円の半径は,音波の波長にくらべて十分小さ いので,B,Dの位置は,音叉の腕の十分近くであると考えてよいでしょう。したがって,音叉の腕が運動し開ききったとき,B,Dの位置の空気分子の変位は 正の向きに最大となります。このとき,B,Dの位置の空気分子の密度は,疎でも密でもないことになります。
音叉が空気を最大の速度(力)で押すのは,腕が閉じた状態から開いた状態へ移る中間のときで,音叉の腕が開ききったとき,腕の速さは0となり腕は空気を 押していません。したがって,音叉の腕の近くの空気が密になるのは, 腕が閉じた状態から開いた状態に移る中間のときで,音叉の腕が開ききったときに腕の付近の空気は疎でも密でもありません。腕が最大の速度で動いたときにで きた密な状態の部分は,腕が開ききったときには,気体分子の玉つきによってλ/4だけ進んでいます。
大阪大学による解説にも「密度変化が変位の微分で与えられることを考えて、変位の傾 きが負になっているところが密である」と書いてあり,上記の図と一致しています。
大阪大学とのやり取り
2018年1月13日の夕方,大阪大学の入試課 入試第一係宛てに,問1もミスではないかと指摘をするメールを送りましたが,返信がなかったので,次に1月19日に理学部宛てにメールを送りました。
それでも返信もなかったので,2月2日に「文部科学省入試ミス対応窓口」にメールを送ったところ,入試ミス対応窓口からは,大阪大学に知らせたとの返信が 2月7日に届きました。
その後,大学に何の動きもなかったため,2月22日に入試課 入試第一係に問い合わせのメールを送ったところ,2月28日に「検証中」とのメールが届きました。
さらに,3月27日,3月29日に続けて催促のメールを送ったところ,3月29日の夕方に,ようやく下記の回答がありました。
大阪大学の検証結果に対する私の見解
大阪大学が言いたいことは,「音叉の腕が運動し開ききったとき,音叉の腕に接した部分の空気の密度は,疎でも密でもないことは認めるが,点 A~Dは音叉から少し離れているので,A,Cは疎,B,Dは密になっている。」ということだと思われます。
ここで,問題文にある「円の中心は音叉の中心Oにあり,その半径は音波の波長にくらべて十分小さく」の「波長にくらべて十分小さく」という言葉が問題になります。
私はこれを,物理は近似であるから,点A〜Dの空気の密度は音叉に接した部分の空気の密度と同じであると近似してよいと解釈しました。したがって,A~D は疎でも密でもないと結論しました。
なお,A-Ⅰでは音叉の大きさについて述べられていませんが,後の問題のA-Ⅲでは「こ の実験では,音叉は十分小さく,点音源と見なせる。」とあります。この仮定の下では,「問題〔3〕の図1 から、点A〜D は⾳叉の腕とは接しておらず、⾳叉よりも有意に外側に位置していることが読み取れます。」と考えたとしても,音叉の周りにある円も波長と比較して点となってしまい,点A〜Dの空気の密度 は音叉に接した空気の密度と同じになります。
次に問題になる言葉は,問題文にある「圧力の高い状態(密)と低い状態(疎)を繰り 返す」という疎密の定義です。大阪大学は,「圧⼒が(振動がない場合 の圧⼒よりも)⾼いか低いかで定義されており、密度が最⾼や最低の状態のみを指しているわけではありません。」と 説明しています。しかし,この疎密の定義は厳密なものではなくアバウトなもので,大阪大学のような解釈はできません。日本語で「高い,低い」は,例えば 「背が高い,背が低い」が平均値より高いか低いかを意味するのではないことは常識です。高校の物理の教科書の音波の図でも, 疎と密という文字はそれぞれ,密度が最も小さい位置と最も大きい位置に記入されています。
また,下の解説の振り⼦の問題やヤングの実験における「十分小さい」という表現は,1次近似(線形近似)ができることを意味します。この問題でどのような 1次近似をし ろというのでしょうか。この問題で近似を用いるならば,0次近似であり,点A〜Dは音叉に接していると近似することになります。
さらに,現実の問題では,空気の変位と密度(圧力)の関係は近似であるので,音叉の形状や振動の状態によっては,点A〜Dでの密度が平均密度より疎である か密であるかが,逆の方向に微妙に変わる可能性もあります。
いずれにしても,物理は近似ですから,点A〜Dのどの点も,疎と密のどちらでもないと考えるのが自然です。
次に,作問をする側になって,(f)が正解となるような問題を作ろうとしてみましょう。
点B,点Dの圧力が振動のない場合の圧力より高くなる条件は,波長をλとしたとき,円の半径rが 0<r<λ/2 を満たすときです。0<r<λ/2を,「(点A〜D を含む円の)半径は⾳波の波⻑にくらべて⼗分⼩さ(い)」などと表現することは私の感覚ではありえません。したがって,問題作成段階では点B,点Dで音叉 に 接する空気も密であると考えていたが,指摘により間違いであることに気が付き,下記の解説の理屈を考えたのではないかと推測されます。
私には,大阪大学の言い分はどれもこれも詭弁で,後付けの理屈としか思えません。私の解説と大学の検証結果に対する見解を読んだ方はどう思われますか?
註
振り子の問題において,「振幅は振り⼦の⽷の⻑さよりも⼗分⼩さい」という場合,振り子が振れる角θが1に比べて十分小さいことより,sinθ≒θ という1次近似を用います。
また,ヤングの干渉実験において,「縞の間隔はスリットとスクリーンの間の距離と⽐べて⼗分⼩さい」という場合,光の行路差対して,xが1に比べて十分小 さいとき (1+x)1/2≒1+x/2 であるという1次近似を用います。
この音波の問題では,「(点A〜D を含む円の)半径は⾳波の波⻑にくらべて⼗分⼩さ(い)」ことから,点A〜Dは音叉付近にあると考えられ,この場合の近似は0次近似であり,この問題に対 して1次近似は使いよ うがありません。
次 に,「⾳叉の腕の表⾯での空気の密度が平均密度である瞬間において、問題〔3〕の図1のように腕から離れた点A〜D での密度は平均密度から変化しており、密、あるいは疎のどちらかをとるということになります。」という主張について考えてみましょう。物理には,数学にお ける厳密な0や「限りなく0に近づく」という概念はありえません。微分におけるdxも,物理においては十分に小さな量と解釈します。圧力,密度,長さ,瞬 間 などを考えるとき,必ず有限の大きさの空気の塊 と有限の長さ,時間を考えます。数学的実数は物理的実体ではなく、物理的実体を表現するために,便宜上導 入されたものです。原子や素粒子の大きさが厳密に0であるとか,物体の長さが小数点以下無限に測定できると考えている物理学者は存在しません。私には,大 阪大学の主張は物理的というより数学的な主張と思えます。
も しも下記の解説を本気で書いたならば「独りよがりな日本語の解釈を押し付ける所は,さすがだ!」となります。いくらなんでも本気ではないと思いますが,出 題 を正当化するために書いたのならば「苦しさは分かりますが,こんな論理で納得する訳がない!」が私の考えです。したがって,私の結論は,この問題は大学の 検証結果と異なり,「与えられた選択肢の中に正解がない。」となります。
また,入試問題においては,問題文がすべてであり,作者の意図を忖度することは不要です。問題文が2通りに解釈できて,解釈により結論が異なれば,出題ミスであるとするのが常識です。
したがって,大阪大学が大学の解説のような意図で出題したとしても,問1は出題ミスであると断言できることになります。
大阪大学の回答
清宮 様
平素は、本学の教育研究活動にご理解・ご協力をいただき御礼申し上げます。
大阪大学教育・学生支援部入試課入試第一係です。
先般いただきました、本学の入試問題に関するご指摘につきまして、検証しました結果を下記のとおりご報告いたします。
今後とも本学の教育研究にご指導、ご鞭撻いただきますよう、お願い申し上げます。
記
○指摘内容
平成29 年度⼤阪⼤学⼀般⼊試(前期⽇程)等における理科問題(物理)〔3〕問1 について、与えられた選択
肢の中に正解がない。
○検証結果
本学の解答例(点A と点C が疎で、点B と点D が密であるとするfが正解)に誤りはないと結論付け
ました。
○解説
(ア) 問題〔3〕の図1 から、点A〜D は⾳叉の腕とは接しておらず、⾳叉よりも有意に外側に位置してい
ることが読み取れます。
⼀⽅で、問題⽂における「(点A〜D を含む円の)半径は⾳波の波⻑にくらべて⼗分⼩さ(い)」という条
件からは、点A〜D における疎や密の状態が⾳叉の近くに⽐べて反転してしまうことがないということが
分かります。
半径が⾳波の波⻑にくらべて⼗分⼩さいという表現は、半径がゼロであることを⽰しているわけではあり
ません。この表現は例えば振り⼦の問題において「振幅は振り⼦の⽷の⻑さよりも⼗分⼩さい」という場
合や、ヤングの⼲渉実験の問題において「縞の間隔はスリットとスクリーンの間の距離と⽐べて⼗分⼩さ
い」という場合と同じです。教科書でこのように表現されたとき、これらの⼩さい量はゼロではなく有限
の量として扱います。
(イ) 「密」や「疎」の定義は問題⽂中で圧⼒が(振動がない場合の圧⼒よりも)⾼いか低いかで定義され
ており、密度が最⾼や最低の状態のみを指しているわけではありません。⾳叉の腕の表⾯での空気の密度
が平均密度である瞬間において、問題〔3〕の図1のように腕から離れた点A〜D での密度は平均密度か
ら変化しており、密、あるいは疎のどちらかをとるということになります。
========
国立大学法人大阪大学
教育・学生支援部
入試課 入試第一係
〒565-0871 大阪府吹田市山田丘1-1
E-mail gakusei-nyusi-dai1@office.osaka-u.ac.jp